#include <itkGaussianSpatialObject.h>
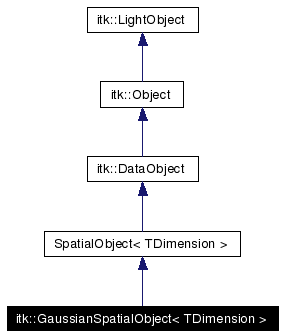
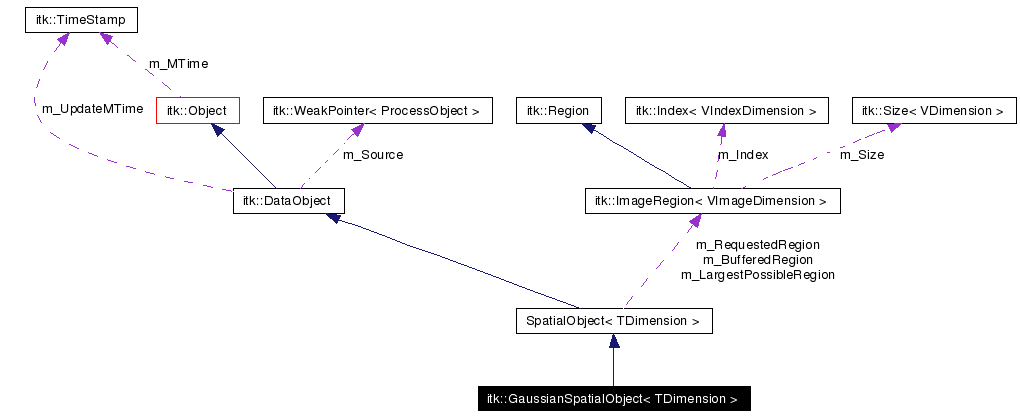
Inheritance diagram for itk::GaussianSpatialObject< TDimension >:
Public Types | |
| typedef GaussianSpatialObject | Self |
| typedef double | ScalarType |
| typedef SmartPointer< Self > | Pointer |
| typedef SmartPointer< const Self > | ConstPointer |
| typedef SpatialObject< TDimension > | Superclass |
| typedef SmartPointer< Superclass > | SuperclassPointer |
| typedef Superclass::PointType | PointType |
| typedef Superclass::TransformType | TransformType |
| typedef Superclass::BoundingBoxType | BoundingBoxType |
Public Member Functions | |
| itkStaticConstMacro (NumberOfDimensions, unsigned int, TDimension) | |
| virtual const char * | GetNameOfClass () const |
| ScalarType | SquaredZScore (const PointType &point) const |
| virtual bool | ValueAt (const PointType &point, ScalarType &value, unsigned int depth=0, char *name=NULL) const |
| virtual bool | IsEvaluableAt (const PointType &, unsigned int, char *) const |
| virtual bool | IsInside (const PointType &point, unsigned int depth, char *name) const |
| virtual bool | IsInside (const PointType &point) const |
| virtual bool | ComputeLocalBoundingBox () const |
| EllipseSpatialObject< TDimension >::Pointer | GetEllipsoid () const |
| virtual void | SetRadius (ScalarType _arg) |
| virtual const ScalarType & | GetRadius () |
| virtual void | SetMaximum (ScalarType _arg) |
| virtual const ScalarType & | GetMaximum () |
Static Public Member Functions | |
| Pointer | New () |
Protected Member Functions | |
| GaussianSpatialObject (void) | |
| ~GaussianSpatialObject (void) | |
| virtual void | PrintSelf (std::ostream &os, Indent indent) const |
Protected Attributes | |
| ScalarType | m_Maximum |
| ScalarType | m_Radius |
The Gaussian function G(x) is given by
![\[ G(\vec{x}) = m e^{-\|\Sigma^{-1} \vec{x}\|^2 / 2}, \]](form_247.png)
where m is a scaling factor set by SetMaximum(), and 
is the (invertible) matrix associated to the IndexToObjectTransform of the object. If is symmetric and positive definite, and m is chosen so that the integral of G(x) is 1, then G will denote a normal distribution with mean 0 and covariance matrix .
Definition at line 46 of file itkGaussianSpatialObject.h.
|
|||||
|
Reimplemented from itk::SpatialObject< TDimension >. Definition at line 60 of file itkGaussianSpatialObject.h. |
|
|||||
|
Reimplemented from itk::SpatialObject< TDimension >. Definition at line 55 of file itkGaussianSpatialObject.h. |
|
|||||
|
Reimplemented from itk::SpatialObject< TDimension >. Definition at line 54 of file itkGaussianSpatialObject.h. Referenced by itk::GaussianSpatialObject< TDimension >::IsEvaluableAt(). |
|
|||||
|
Reimplemented from itk::SpatialObject< TDimension >. Definition at line 58 of file itkGaussianSpatialObject.h. Referenced by itk::GaussianSpatialObject< TDimension >::IsEvaluableAt(). |
|
|||||
|
Reimplemented from itk::SpatialObject< TDimension >. Definition at line 53 of file itkGaussianSpatialObject.h. Referenced by itk::GaussianSpatialObject< TDimension >::IsEvaluableAt(). |
|
|||||
|
Standard class typedefs. Reimplemented from itk::SpatialObject< TDimension >. Definition at line 52 of file itkGaussianSpatialObject.h. |
|
|||||
|
Reimplemented from itk::SpatialObject< TDimension >. Definition at line 56 of file itkGaussianSpatialObject.h. |
|
|||||
|
Definition at line 57 of file itkGaussianSpatialObject.h. |
|
|||||
|
Reimplemented from itk::SpatialObject< TDimension >. Definition at line 59 of file itkGaussianSpatialObject.h. |
|
||||||||||
|
|
|
||||||||||
|
|
|
|||||||||
|
This function needs to be called every time one of the object's components is changed. Reimplemented from itk::SpatialObject< TDimension >. |
|
|||||||||
|
Returns the sigma=m_Radius level set of the Gaussian function, as an EllipseSpatialObject. |
|
|||||||||
|
The maximum value of the Gaussian (its value at the origin of the spatial object coordinate system). |
|
|||||||||
|
Run-time type information (and related methods). Reimplemented from itk::SpatialObject< TDimension >. |
|
|||||||||
|
The Radius determines the bounding box, and which points are considered to be inside the SpatialObject. All points with z-score less than the radius are in the object. |
|
||||||||||||||||||||
|
Always returns true since a Gaussian can be evaluated anywhere. Reimplemented from itk::SpatialObject< TDimension >. Definition at line 92 of file itkGaussianSpatialObject.h. References itk::GaussianSpatialObject< TDimension >::m_Maximum, itk::GaussianSpatialObject< TDimension >::m_Radius, itk::GaussianSpatialObject< TDimension >::Pointer, itk::GaussianSpatialObject< TDimension >::PointType, and itk::GaussianSpatialObject< TDimension >::ScalarType. |
|
||||||||||
|
Test whether a point is inside or outside the object For computational speed purposes, it is faster if the method does not check the name of the class and the current depth |
|
||||||||||||||||||||
|
Test whether a point is inside or outside the object Reimplemented from itk::SpatialObject< TDimension >. |
|
||||||||||||||||||||
|
|
|
|||||||||
|
Method for creation through the object factory. Reimplemented from itk::SpatialObject< TDimension >. |
|
||||||||||||||||
|
Print the object information in a stream. Reimplemented from itk::SpatialObject< TDimension >. |
|
||||||||||
|
The maximum value of the Gaussian (its value at the origin of the spatial object coordinate system). |
|
||||||||||
|
The Radius determines the bounding box, and which points are considered to be inside the SpatialObject. All points with z-score less than the radius are in the object. |
|
||||||||||
|
If the matrix S is returned by this->GetIndexToObjectTransform()->GetMatrix(), then SquaredZScore(x) returns |Sx| squared. |
|
||||||||||||||||||||||||
|
Returns the value of the Gaussian at the given point. |
|
|||||
|
Definition at line 118 of file itkGaussianSpatialObject.h. Referenced by itk::GaussianSpatialObject< TDimension >::IsEvaluableAt(). |
|
|||||
|
Definition at line 119 of file itkGaussianSpatialObject.h. Referenced by itk::GaussianSpatialObject< TDimension >::IsEvaluableAt(). |
1.3.5 written by Dimitri van Heesch,
© 1997-2000